CU Mechanical Engineering Statics and Structures Matlab tutorials

---

Writing Matlab Functions: computing reaction internal shear force and bending moment

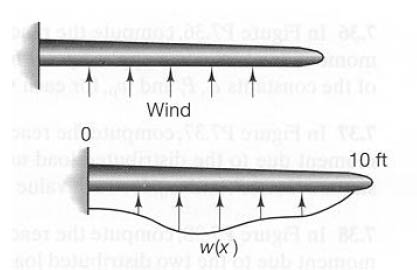
The ability to write custom functions within Matlab lends an extraordinary amount of power to the user. In this example, we will write a function that will compute the reaction forces and the internal shear force and bending moment for an airplane wing. A lifting load on an airplane wing is modeled by w(x) =1000 x sin(x)lb / ft , and the wing is modeled as a 10-ft-long cantilevered beam. We will also plot the shear force and the bending moment as a function of x.

The variables used in this function will be defined as follows:

Variable	Remarks	Status
--------	-------	------
w	Distributed load	Given
A	Area under the load curve	To be computed
L	Length of the beam	Given
AInc	Increments to change the length'L'	Given

We will begin by establishing default values for the parameters of this function, as outlined below:

L = 10;
w = 1000;
AInc = 0.1;
AngleToRadians = pi/180;

To calculate the total force acting on the beam we need to integrate the distributed load w(x) along the length of the beam. The total load is the area under the curve of the load w(x). Consider a vertical strip of infinitesimally small thickness 'dx' at any 'x' having length of 'w(x)'. Let the area of this strip be dA = w(x)dx. As this strip moves along the x axis from '0' to 'L', we need to integrate the above equation dA from '0' to 'L'.

x=0:0.1:10;
n = length(x);

This defines the length of the array 'x'.

At this point you can use the quad8 function for numerical integration:

for i = 1:n
    Vx(i) = quad8 ('fV731',0,x(i),[],[],w,L);
    Mx(i) = quad8 ('fB731',0,x(i),[],[],w,L);
end

You may now prepare to plot your data:

figure(1); clf;
subplot (2,1,1)
plot (x,Vx)
xlabel ('x (ft)')
ylabel ('V(x) (lb)')
subplot (2,1,2)
plot (x,Mx)
xlabel ('x (ft)')
ylabel ('M(x) (lb-ft)')

The first is a plot of the shear force diagram; the second is a plot of the bending moment diagram.

---