CU Mechanical Engineering Statics and Structures Matlab tutorials

---

Writing Matlab Scripts: Computing forces on a truss

Writing Matlab m-files is another way to compile a series of Matlab commands into one script and is often necessary when performing complicated computations. The structure is slightly different than a function in that no values are returned and you do not pass values to the script. Commands can be entered into a scrip m-file just as they would be typed at the command prompt.

In this tutorial, we will examine the forces on a truss structure seen in the figure below and the following problem: Consider the cantilevered truss as sketched in the figure below, and calculate the forces in each member if a wind load of approximately 1000 N is added at joint D. That is, let L1 =1000N, L2 = 500N, and L N 3 =1000 . State which members are in tension and which are in compression, and determine the reaction forces as well.

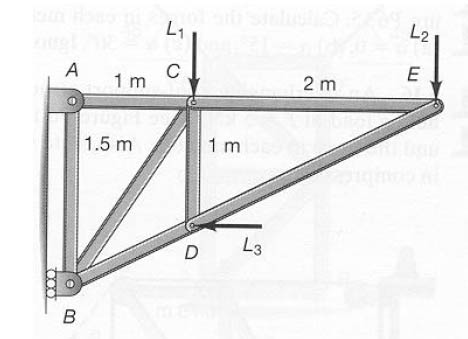
The variables used in this function will be defined as follows:

Variable	Remarks	Status
--------	-------	------
L1,L2,L3	Forces applied at joints C, E, D respectively	To be computed
Lac,Lab,Lcd,Lce	Lengths of different truss members	To be computed
Fac,Fab,Fcd,Fce	Forces in different truss members	To be computed
Fbc,Fdb,Fde	Forces in different truss members	To be computed
Theta1	Angle between CE and DE	To be computed
Theta2	Angle between AC and BC	To be computed
Theta3	Angle between BC and BD	To be computed
Rxa	Reaction at point A along X axis	To be computed
Rya	Reaction at point A along Y axis	To be computed
Rxb	Reaction at point B along X axis	To be computed
Ryb	Reaction at point B along Y axis	To be computed

We will begin by establishing default values for the parameters of this function, as outlined below:

L1 = 1000;
L2 = 500;
L3 = 1000;
Lac = 1; Lce = 2; Lab = 1.5; Lcd = 1;

The first task is to compute the angles. To do so, we input the following:

Theta1 = atan(Lcd/Lce);
Theta2 = atan(Lab/Lac);

Using equilibrium calculations, we can analyze the forces acting on each joint, one at a time. We start by considering the equilibrium at joint E:

Fed = L2/sin(Theta1);
Fce = Fed*cos(Theta1);

Next, consider the equilibrium of joint D:

Fdb = (Fed*cos(Theta1)+L3)/cos(Theta1);
Fcd = Fdb*sin(Theta1) - Fed*sin(Theta1);

Now consider the equilibrium of joint C:

Fcb = (L1 - Fcd)/sin(Theta2);
Fca = Fcb*cos(Theta2) + Fce;

Finally, consider the equilibrium of joint B:

Fba = Fcb*sin(Theta2) + Fdb*sin(Theta1);

We finish by computing the support reactions:

Rax = Fca;
Ray = Fba;
Rbx = Fdb*cos(Theta1) + Fcb*cos(Theta2);
Rby = 0;

Finally, display your results with the following commands:

fprintf('The forces in members are: Fec = %gN(T)\nFed = %gN(C)\n',...
		Fce, Fed);
fprintf('Fdc = %gN(C)\nFdb = %gN(C)\nFbc = %gN(C)\nFba = %gN(T)\n',...
		Fcd, Fdb, Fcb, Fba);
fprintf('Fca = %gN(T)\n',Fca);

---