University of Colorado ::: Mechanical Engineering

CU Mechanical Engineering

Statics and Structures Matlab tutorials

Writing Matlab Scripts: forces on a folding platform

Writing Matlab m-files is another way to compile a series of Matlab commands into one script and is often necessary when performing complicated computations. The structure is slightly different than a function in that no values are returned and you do not pass values to the script. Commands can be entered into a scrip m-file just as they would be typed at the command prompt.

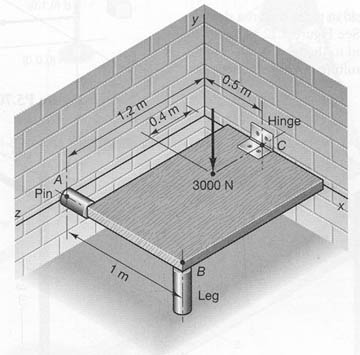
In this tutorial, we will examine the forces on the folding platform seen in the figure below and the following problem: A folding platform is used to hold parts, as well as to conserve floor space when not in use. The platform is supported by a hinge at C, which is assumed to support negligible moments, a leg at B, modeled as a frictionless support, and a removable pin at A, modeled as a thrustless bearing, again with negligible moments. If the platform is loaded as illustrated in the figure below, compute the reaction forces at A, B, and C. Ignore the thickness of the platform.

The variables used in this function will be defined as follows:

Variable	Remarks	Status
--------	---------	------
P	Applied vertical force (at D)	Given
O	Point O is the origin	Given
A,B,C,D	X,Y,Z coordinates of points A,B,C,D	Given
X	Reactions at A,B,C	To be computed

We will begin by establishing default values for the parameters of this function, as outlined below:

P(1) = 0; P(2) = -3000; P(3) = 0;
A(1) = 0; A(2) = 0; A(3) = 1.2;
B(1) = 1; B(2) = 0; B(3) = 1.2;
C(1) = 0.5; C(2) = 0; C(3) = 0;
D(1) = 0.5; D(2) = 0; D(3) = 0.4;
Ra(1) = 0; Ra(2) = 1; Ra(3) = 1;
Rb(1) = 0; Rb(2) = 1; Rb(3) = 0;
Rc(1) = 1; Rc(2) = 1; Rc(3) = 1;

There are six unknowns (Ray, Raz, Rby, Rcx, Rcy, Rcz) and six equations of equilibrium that we can write as S X = Q

for i=1:1:6
    Q(i) = 0;
    for j=1:1:6
        S(i,j) = 0;
    end;
end;

The force equilibrium equations can be written as follows:

S(1,4) = 1;
S(2,1) = 1; S(2,3) = 1; S(2,5) = 1;
S(3,2) = 1; S(3,6) = 1;

The moments about the hinge c are:

S(4,1) = -1.2; S(4,3) = -1.2;
S(5,2) = 0.5;
S(6,1) = -0.5; S(6,3) = 0.5;
Rdc = D - C;
M = cross (Rdc, P);

To generate the vector for the right-hand side, type:

Q = [-P(1); -P(2); -P(3); -M(1); -M(2); -M(3)];

To complete and solve this problem, type:

X = inv(S)*Q;

Finally, display your results with the following commands:

fprintf ('The (y,z) reactions at point A are ');
fprintf ('%g N and %g N\n', X(1), X(2));
fprintf ('The (y) reaction at point B is ');
fprintf ('%g N\n', X(3));
fprintf ('The (x,y,z) reactions at point C are ');
fprintf ('%g N, %g N and %g N\n', X(4), X(5), X(6));