CU Mechanical EngineeringNumerical Methods Matlab tutorials |
Writing Matlab Scripts: solving for the root of a nonlinear equation
In this example, we will write a function that finds a root of a nonlinear equation using (a) bisection method, (b) secant method, and (c) Newton’s method. Each of these methods will be defined as separate functions.
Unlike functions, scripts in Matlab do not require any initial statements - they are simply a collection of commands run serially. In essence, you could get the same thing by typing the lines one after the other at the command line however the power of scripts lies in the fact that changes and interations are simple and the time savings are well worth the work. This script to solve the roots of nonlinear equtions begins by defining several variables to be used later on:
syms f x eps =0.00001;
The 'syms' command is a way to construct symbolic objects. The 'eps' variable is the tolerance for finding a root.
This project requires two major steps: the case considering the function exp(x)-2 and another case considering the function atan(x-1/sqrt(2)). The code for the first case looke like this:
% Case a:
f=exp(x)-2;
[x_root_bisec,x_bisec,f_bisec]=bisection(0,1,f,eps);
[x_root_secant,x_secant,f_secant]=secant(0,1,f,eps);
[x_root_newton,x_newton,f_newton]=newton(1,f,eps);
disp(['x_exact=',num2str(log(2)),' x_bisection=',num2str(x_root_bisec),...
' x_secant=',num2str(x_root_secant),' x_newton=',num2str(x_root_newton)])
figure(1)
hold off
semilogy(abs(f_bisec),'r-')
ylabel('error')
xlabel('iteration')
hold on
plot(abs(f_secant),'m-')
plot(abs(f_newton),'b-')
This script utilizes functions external to this script. It is important to note that inline functions can only be used within functions and not scripts. for case (a), the function is defined and then each of the functions are called. The next segment of code plots the results from the first case. The 'figure(1)' command tells matlab that the following commands are for a single plot. The plot is identified to be a semi-log plot with the log scale on the y-axis. The 'hold on' command indicates that all following plot commands will be plotted on the same graph.
Since there are three ways to evaluate this root, it is necessary to look at each way seperately. Each has it's own block of code. The first is the bisection:
function [x_root,x_guess,f_guess]=bisection(x1,x2,fun,eps)
The function declaration for these different methods generally take four inputs including the interval, the function and the tolerance value.
xh1=min([x1 x2]);
xh2=max([x1,x2]);
x_guess = [xh1 xh2];
f_guess = subs(fun,x_guess);
if (f_guess(1)*f_guess(2)) > 0
disp('wrong guess');
x_root=NaN;
return
end
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
disp('excellent guess')
return
end
iter = 2;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=(xh1+xh2)/2;
f_guess(iter) = subs(fun,x_guess(iter));
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
check = logical(0);
else
if f_guess(iter) < 0
xh1=x_guess(iter);
elseif f_guess(iter) > 0
xh2=x_guess(iter);
end
end
end
The fist part of the above segment looks at the first two arguments of the function to determine the interval and defines that interval as the vector 'x_guess'. The next line uses the 'subs' built-in matlab function to evaluate the given function with the values in the 'x_guess' vector and then determines if either one of those points are within the tolerance value of zero. If so, it returns the value and uses the 'return' command to stop the script. This part also determines if the function values at the endpoints of the interval are diffenrent signs. If not, the script terminates with errors.
The following 'while' loop begins the iteration process to converge on a solution. It begins by taking the initial interval and dividing it in half and evaluating the new midpoint to determine if it is a root. If not, the sign is compared at that point to both of the end points to determine the interval it will use for the next iteration. This loop continues to bisect the intervals, always evaluating at the midpoint until the function value at that point is within the tolerance of zero at which point the root is returned.
function [x_root,x_guess,f_guess]=secant(x1,x2,fun,eps)
This function takes the same inputs as the secant method: interval values, function and prespecified tolerance.
xh1=min([x1 x2]);
xh2=max([x1,x2]);
x_guess = [xh1 xh2];
f_guess = subs(fun,x_guess);
fh1=f_guess(1);
fh2=f_guess(2);
if (f_guess(1)*f_guess(2)) > 0
disp('wrong guess');
x_root=NaN;
return
end
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
disp('excellent guess')
return
end
iter = 2;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=xh1-fh1*(xh1-xh2)/(fh1-fh2);
f_guess(iter) = subs(fun,x_guess(iter));
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
check = logical(0);
else
if f_guess(iter) < 0
xh1=x_guess(iter);
fh1=f_guess(iter);
elseif f_guess(iter) > 0
xh2=x_guess(iter);
fh2=f_guess(iter);
end
end
end
This function begins in the same way as the secant method by evaluating the end points of the interval. If neither of these points are roots, the iterations begin by running the secant algorithm for determining roots. The while loop systematically guesses and evaluates the function at those values to determine if it has found a root. If not, the algorithm continues until a root within the tolerance if found.
Finally there is the Newton Method:
function [x_root,x_guess,f_guess]=newton(x1,fun,eps)
x_guess(1) = [x1];
f_guess(1) = subs(fun,x_guess);
df=subs(diff(fun),x_guess(1));
if abs(f_guess) < eps
x_root=x_guess;
disp('excellent guess');
return
end
iter = 1;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=0;
f_guess(iter)=0;
x_guess(iter)=x_guess(iter-1)-f_guess(iter-1)/df;
f_guess(iter) = subs(fun,x_guess(iter));
df=subs(diff(fun),x_guess(iter));
if abs(f_guess(iter)) < eps
x_root=x_guess(iter);
check = logical(0);
end
end
Once again, the beginning of this function is the same as the previous two methods. The next section uses the 'diff' function to calculate the derivitive of the input function. The 'subs' function is once again used to dermine the value at this point.
Now we'll consder the second case, when the function is defined as atan(x-1/sqrt(2)):
%Case b:
f=atan(x-1/sqrt(2));
[x_root_bisec,x_bisec,f_bisec]=bisection(0,1,f,eps);
[x_root_secant,x_secant,f_secant]=secant(0,1,f,eps);
[x_root_newton,x_newton,f_newton]=newton(1,f,eps);
disp(['x_exact=',num2str(log(2)),' x_bisection=',num2str(x_root_bisec),...
' x_secant=',num2str(x_root_secant),' x_newton=',num2str(x_root_newton)])
figure(2)
hold off
semilogy(abs(f_bisec),'r-')
ylabel('error')
xlabel('iteration')
hold on
plot(abs(f_secant),'m-')
plot(abs(f_newton),'b-')
This is the same as the first example but using a different function. Refer to the above for more in depth detail.
The m-file can now be saved as 'root.m' The following are several sample outputs from the code illustrating the ways to call the function with different types of return arguments.
>> root x_exact=0.69315 x_bisection=0.69315 x_secant=0.69315 x_newton=0.69315 x_exact=0.69315 x_bisection=0.70711 x_secant=0.70711 x_newton=0.70711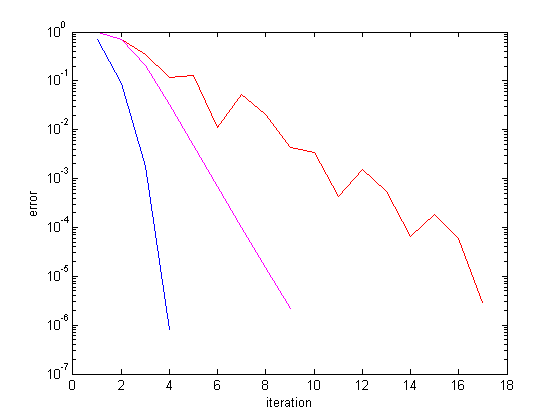
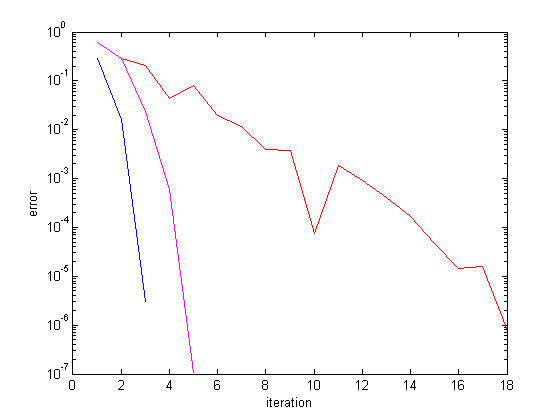
The entire matlab script can be seen below or downloaded here (right-click to save):
%******************************************************************************
%* Computational Project # 2 *
%******************************************************************************
syms f x
eps =0.00001;
% Case a:
f=exp(x)-2;
[x_root_bisec,x_bisec,f_bisec]=bisection(0,1,f,eps);
[x_root_secant,x_secant,f_secant]=secant(0,1,f,eps);
[x_root_newton,x_newton,f_newton]=newton(1,f,eps);
disp(['x_exact=',num2str(log(2)),' x_bisection=',num2str(x_root_bisec),..
' x_secant=',num2str(x_root_secant),' x_newton=',num2str(x_root_newton)])
figure(1)
hold off
semilogy(abs(f_bisec),'r-')
ylabel('error')
xlabel('iteration')
hold on
plot(abs(f_secant),'m-')
plot(abs(f_newton),'b-')
% Case b:
f=atan(x-1/sqrt(2));
[x_root_bisec,x_bisec,f_bisec]=bisection(0,1,f,eps);
[x_root_secant,x_secant,f_secant]=secant(0,1,f,eps);
[x_root_newton,x_newton,f_newton]=newton(1,f,eps);
disp(['x_exact=',num2str(log(2)),' x_bisection=',num2str(x_root_bisec),...
' x_secant=',num2str(x_root_secant),' x_newton=',num2str(x_root_newton)])
figure(2)
hold off
semilogy(abs(f_bisec),'r-')
ylabel('error')
xlabel('iteration')
hold on
plot(abs(f_secant),'m-')
plot(abs(f_newton),'b-')
%-------------------------------------------------------------
%Bisection
function [x_root,x_guess,f_guess]=bisection(x1,x2,fun,eps)
xh1=min([x1 x2]);
xh2=max([x1,x2]);
x_guess = [xh1 xh2];
f_guess = subs(fun,x_guess);
if (f_guess(1)*f_guess(2)) > 0
disp('wrong guess');
x_root=NaN;
return
end
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
disp('excellent guess')
return
end
iter = 2;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=(xh1+xh2)/2;
f_guess(iter) = subs(fun,x_guess(iter));
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
check = logical(0);
else
if f_guess(iter) < 0
xh1=x_guess(iter);
elseif f_guess(iter) > 0
xh2=x_guess(iter);
end
end
end
%----------------------------------------------------------
%Secant
function [x_root,x_guess,f_guess]=secant(x1,x2,fun,eps)
xh1=min([x1 x2]);
xh2=max([x1,x2]);
x_guess = [xh1 xh2];
f_guess = subs(fun,x_guess);
fh1=f_guess(1);
fh2=f_guess(2);
if (f_guess(1)*f_guess(2)) > 0
disp('wrong guess');
x_root=NaN;
return
end
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
disp('excellent guess')
return
end
iter = 2;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=xh1-fh1*(xh1-xh2)/(fh1-fh2);
f_guess(iter) = subs(fun,x_guess(iter));
if min(abs(f_guess)) < eps
[f_min,i_min] = min(abs(f_guess));
x_root=x_guess(i_min);
check = logical(0);
else
if f_guess(iter) < 0
xh1=x_guess(iter);
fh1=f_guess(iter);
elseif f_guess(iter) > 0
xh2=x_guess(iter);
fh2=f_guess(iter);
end
end
end
%------------------------------------------------------
%Newton
function [x_root,x_guess,f_guess]=newton(x1,fun,eps)
x_guess(1) = [x1];
f_guess(1) = subs(fun,x_guess);
df=subs(diff(fun),x_guess(1));
if abs(f_guess) < eps
x_root=x_guess;
disp('excellent guess');
return
end
iter = 1;
check = logical(1);
while check
iter = iter +1;
x_guess(iter)=0;
f_guess(iter)=0;
x_guess(iter)=x_guess(iter-1)-f_guess(iter-1)/df;
f_guess(iter) = subs(fun,x_guess(iter));
df=subs(diff(fun),x_guess(iter));
if abs(f_guess(iter)) < eps
x_root=x_guess(iter);
check = logical(0);
end
end